

David Bachmann, Vyacheslav Shatokhin
Free space quantum communication, or transmission of quantum information from one place to another through the atmosphere, can be realized using the two-dimensional, polarization degree of freedom of photons. However, higher-dimensional quantum systems, also referred to as qudits, present several advantages over simple two-level systems (qubits). The first benefit of high-dimensional states is their capability of naturally increasing the information content encoded in a single carrier. Moreover, when compared to qubits, qudits are more robust against quantum cloning and, thus, they allow to enhance the security of quantum key distribution (QKD).
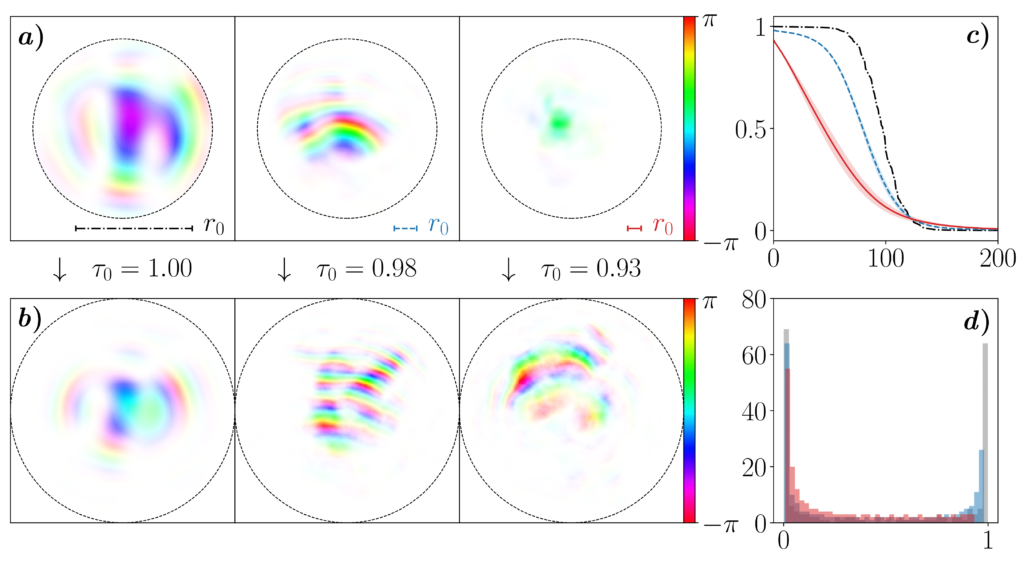
One of the promising candidates for the realization of such qudits are photonic orbital angular momentum (OAM) states, which span a discrete, infinite-dimensional Hilbert space. On the down side, the defining feature of OAM-carrying light beams, their helical wavefront, is fragile with respect to turbulence-induced refractive index fluctuations. We theoretically study the potential of adaptive optics (AO) to protect high-dimensional photonic OAM states against turbulence-induced phase distortions.
We also explore the alternative possibility of high-dimensional spatial encoding — into highly transmissive eigenmodes of a random realization of atmospheric turbulence. Our work shows that such modes offer significantly improved high-fidelity signal transmission as compared to standard encoding bases corrected by AO. Furthermore, in dynamic turbulence the eigenmodes exhibit slow subdiffusive algebraic decay of the transmitted power with the communication time.
Heinz-Peter Breuer
We study the foundations of the quantum theory of open systems, i.e., of quantum systems coupled to an environment, featuring a large variety of physical phenomena such as dissipation, decoherence, relaxation to thermal equilibrium and emergence of nonequilibrium stationary states. Important achievements in recent years are the characterization and quantification of memory effects through the flow of information between an open quantum system and its environment, and the development of various schemes for the detection of quantum correlations by local operations. Current research topics are, in particular, Markovian and non-Markovian quantum processes in many-body systems, and the foundations of nonequilibrium quantum thermodynamics.
[1] Non-Markovian dynamics in open quantum systems
H.-P. Breuer, E.-M. Laine, J. Piilo and B. Vacchini
Rev. Mod. Phys. 88, 021002 (2016)
[2] Open-system approach to nonequilibrium quantum thermodynamics at arbitrary coupling
Alessandra Colla and Heinz-Peter Breuer
Phys. Rev. A 105, 052216 (2022)
Giorgio Ciliberto
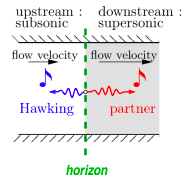
In an acoustic analogue system, as the ones obtained in BECs, a transonic fluid flow (i.e. a flow which is supersonic in a region of space, and subsonic elsewhere) is experimentally implemented in order to model a gravitational black hole. Quantum fluctuations of the sound field induce emission of Hawking quanta away from the acoustic horizon. This radiation is correlated to a “partner” which falls inside the analogous black hole. This is why studying this phenomenon in Bose-Einstein condensates allows for a better understanding of multipartite entanglement and information transport. The topic therefore belongs to the very active and stimulating area of research called “quantum simulators”.
Eric Brunner, Edoardo Carnio, Christoph Dittel, Vyacheslav Shatokhin, Andreas Woitzik
Quantum computation describes the implementation of algorithms using quantum mechanical systems and their ability to exhibit interference. Expectations placed on this technology were fueled by the discovery of a (small) number of quantum algorithms which can solve particular problems faster than any classical computer. A famous example is Shor’s algorithm, which theoretically allows factoring large numbers efficiently, a task that so far gives any classical computer a hard time.
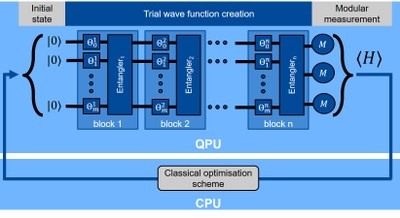
However, practical implementations of quantum algorithms remain challenging due to the fragility of quantum systems under environmental influences. Circumventing this problem requires appropriate error correction procedures, which are out of reach with current technology. Therefore, some contemporary approaches to quantum computing combine noisy intermediate-scale quantum devices and classical computing units with the hope to find possible advantages without the need of expensive error correction.
We investigate these hybrid algorithms, with a focus on a detailed understanding of quantum information processing and its role for quantum computational models. Inter alia, we perform numerical studies to uncover the basic properties of various algorithms with respect to information theoretic quantities such as the production of entanglement or the speed of convergence. QOS is involved in the Competence Center Quantum Computing Baden-Württemberg, which allows us (together with partners from Fraunhofer IWM, IAF and EMI, and from the University of Ulm) to test the performance of elementary pieces of code on IBM’s Quantum System One at Ehningen.
Edoardo Carnio, Frieder Lindel, Andreas Woitzik
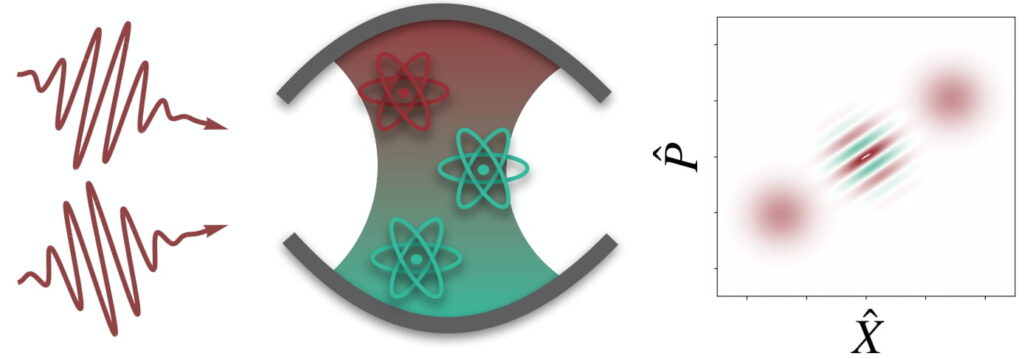
The control of quantum processes in physics, chemistry or material science constitutes the premise of impending quantum-based technology: from the quantum computer, to quantum sensors, to simulation platforms. This task is usually achieved by preparing the target system in a specific initial state and then driving it, via a control field, into a desired target state. The efficiency of this operation can be significantly increased by tailoring the control field, normally a combination of laser pulses, in its classical properties (e.g., phase, amplitude, duration, polarization).
If the control field is also quantized, however, we have many more parameters (as many as the Hilbert space dimension) which we can tune to optimally drive a transition in the target system. We investigate whether, and under which circumstances, such an optimal quantized control outperforms the classical counterpart.
The setup we consider is that of one or more atoms placed in, or travelling through, a cavity. Thanks to the coupling between the discrete atomic levels and a cavity mode, we can either (i) prepare the cavity state to optimally drive the atom(s) from an initial to a final state [1] or (ii) prepare the state of a chain of atoms to drive the cavity from an initial to a desired target state (cfr. the micromaser [2]). In these scenarios we then study how the quantum nature of the control field (e.g., a sub-Poissonian photon number distribution of the cavity state, entanglement in the atomic chain) helps achieving the control task.
[1] F. Lindel, E. G. Carnio, S. Y. Buhmann, A. Buchleitner, arXiv:2208.13548 (2022)
[2] B.-G. Englert, arXiv:quant-ph/0203052 (2002).
Christoph Dittel
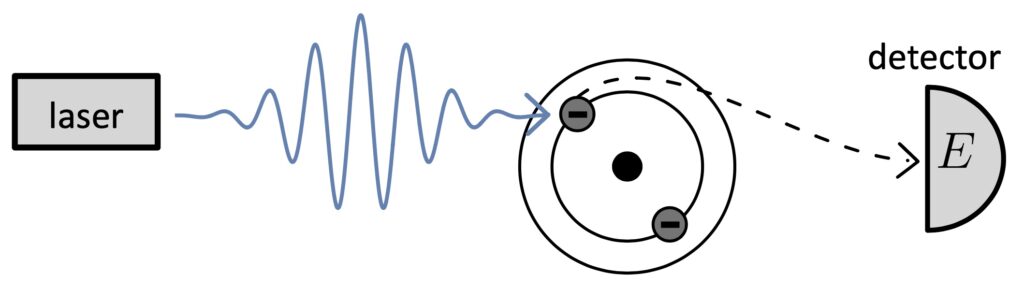
With the aim of resolving electronic dynamics in atoms and molecules, experimentalists developed laser systems which generate ultrashort laser pulses (of attosecond duration) in the extreme-ultraviolet (XUV) regime. By shooting such laser pulses on a target atom, the absorption of a single photon suffices in order to ionize the atom. Now, by sending in an additional infrared (IR) laser pulse on top of the XUV pulse and recording the energy of the photoelectron as a function of the phase between the IR and XUV light fields, one can observe an interference signal. While this directly shows that photoionization is a coherent process, the underlying experimental technique ultimately allows for the investigation of coherent quantum mechanical phenomena in light-matter interactions. In our research, we are particularly interested in using this interference technique to probe fundamental physics. This includes quantum state tomography of photoelectrons, tests of quantum mechanical principles, and the investigation of entanglement in photoionization.
Lucas Weitzel, Dominik Lentrodt
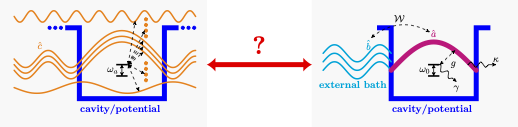
Resonance theory is a well-established concept in quantum mechanics and general wave propagation theory alike. At its heart lies the idea of extracting the relevant features – the resonances – from a complex system often featuring a continuous spectrum. This idea is also of great value in the study of second quantized systems, where continuous spectra often lead to intractable complexity. While under certain assumptions, such problems can be simplified, e.g. using master equations from the theory of open quantum systems, such approaches can fail for extreme coupling strengths or large losses.
We currently focus on incorporating ideas from resonance theory into the framework of open quantum systems. In the study of cavity QED, such approaches have already been used for decades in the form of so-called few mode models, such as the seminal single mode Jaynes-Cummings model. Our work establishes a general theoretical framework for when such models can be used and in which settings they break down.
In particular, we consider realistic complex resonators and what conditions the underlying wave equations (e.g., Schrödinger’s equation with a potential or Maxwell’s equations with a dielectric medium) impose on these open system models. Our work therefore lies at the interface of resonance and open quantum systems theory, with applications ranging from cavity-modified chemistry and quantum plasmonics to potentially gravitational systems.
Fabian Spallek
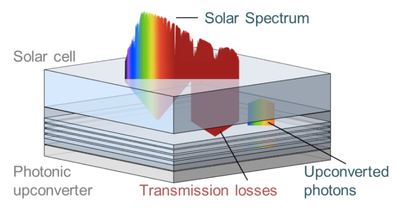
The term upconversion denotes processes which convert two low-energy photons into one photon with higher energy, and can be used in a wide range of optical applications. One promising concept is to combine upconverter materials with silicon solar cells to improve their efficiency by utilizing the full range rather than only a fraction of the solar spectrum. The quantum yield, which quantifies the overall efficiency of an upconverter material, is determined by an interplay of emission rates, energy transfer processes, local irradiance and local density of states. Embedding the upconverter material in photonic dielectric nanostructures allows one to affect all of these determining factors and thus to influence and improve the overall efficiency of the upconversion process.
By quantifying the structure’s influence on the basic underlying processes, we develop models that allow to optimize structures for upconversion efficiency. In particular, we consider arbitrary finite multilayered dielectric stacks and utilize methods from macroscopic QED to calculate energy transfer rates, the local density of states and the structure’s influence on spontaneous emission and absorption rates of the upconverter ions. For example, by tuning the thickness of each individual layer in a multi-layered photonic structure, it is possible to trap incident photons of a given wavelength inside this structure, and considerably increase the local irradiance. Our models, rooted in analytical methods in combination with numerical optimization algorithms, allow us to propose specific designs optimized for upconversion efficiency.
To utilize our results for practical applications and to compare our predictions with experimental data, we collaborate with experimentalists at Fraunhofer Institute for Solar Energy Systems.
Eric Brunner, Christoph Dittel, Gabriel Dufour
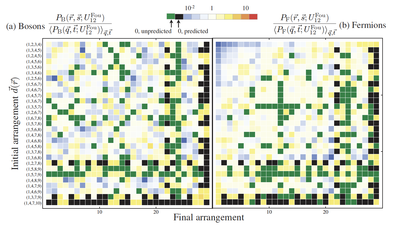
The dynamics of many identical particles such as photons or cold atoms is governed by unique interference effects. For example, two indistinguishable photons impinging on opposite sides of a semi-transparent mirror (i.e., a beam splitter) always emerge on the same side, as if tossing two coins always gave twice heads or twice tails, but never one of each.
This interference rests upon the particles’ indistinguishability (see the research topic “Indistinguishability”). It represents a genuine many-particle effect that becomes highly intricate when adding more and more particles to the dynamical evolution, and ultimately allows for diverse applications in quantum simulation and quantum computation.
In our research, we are broadly interested in this interference effect. For example, we study how symmetries simplify the dynamical behavior, how interactions between the particles affect many-particle interference, how random evolutions reveal interesting properties of the many-body quantum state, and how the particles’ coupling to an environment (in an open quantum system) deteriorates their ideal interference dynamics.
Dominik Lentrodt
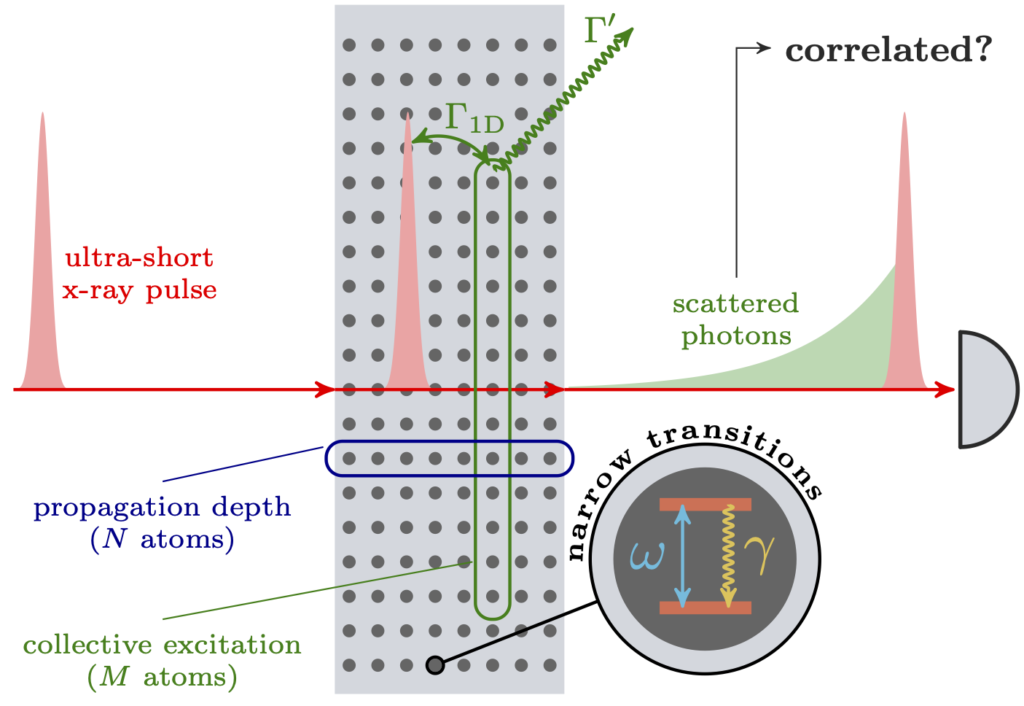
In other projects of the group, much of the focus lies on correlations between different quantum mechanical degrees of freedom. Here, we study how to create such correlations in realistic many-body systems.
In particular, we consider the transport of multi-photon states through lattices containing narrow transitions – i.e. qubits with very low decoherence. The many-body character of this setup and our interest in quantum mechanical correlation functions of the photon field make this a challenging problem to address theoretically. The experimental motivation is that such systems may allow to create non-classical photon states in the hard x-ray range and to thereby unlock quantum optics in a previously unexplored regime of high-energy photons.
Jonathan Brugger, Christoph Dittel
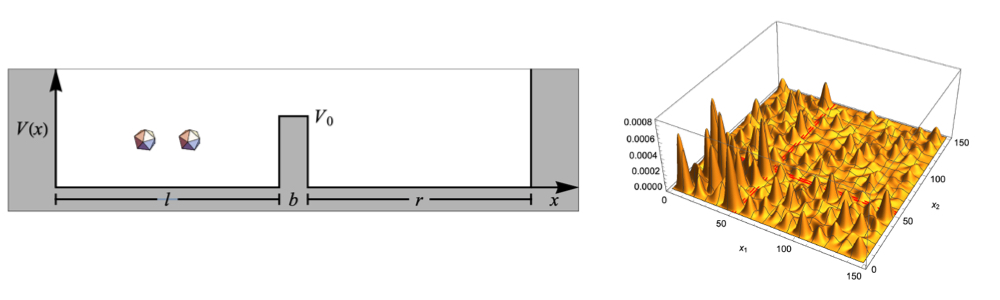
Understanding the exact quantum tunneling dynamics of few interacting particles is not only relevant for fundamental physics, it is likewise important for microelectronics, when circuit sizes are scaled down such that quantum effects become non-negligible. The simplest model constitutes the tunneling of few particles through the barrier of a one-dimensional double-well potential. While for non-interacting particles the Schrödinger equation of this problem can be solved analytically, once we include interactions, already for two particles no solution to the corresponding Schrödinger equation is known. In this case, we have to tackle the problem numerically. To this end, in our research we use so-called finite element methods (which are well studied and commonly used for simulations in applied mathematics) through which we can numerically solve the Schrödinger equation up to machine precision. This allows us to exactly simulate quantum tunneling of interacting few-particle systems, even beyond ground state dynamics (i.e. even for initially excited states). Some questions addressed in this context aim at understanding the role of the particles’ initial state as well as their interaction potential (e.g. contact vs. Coulomb interaction) for the tunneling dynamics, and the emergence of non-Markovianity (i.e. the backflow of information) in the tunneling process.
Edoardo Carnio, Vyacheslav Shatokhin
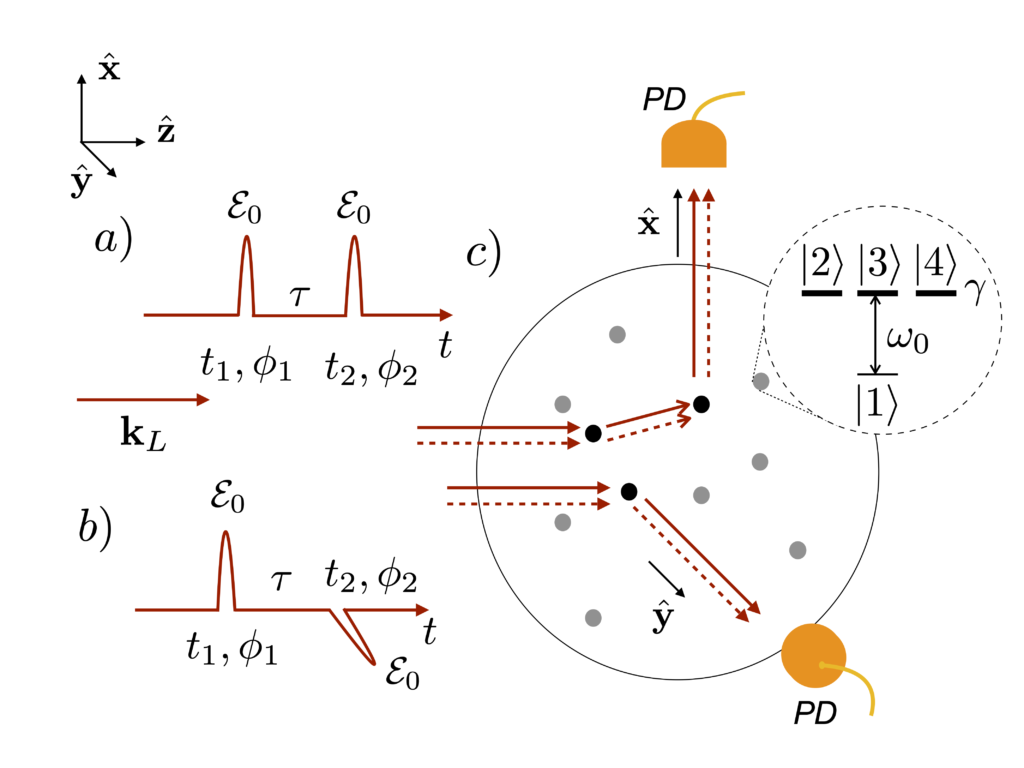
Dipole-dipole interactions in atomic ensembles are of paramount fundamental and practical importance in atomic, molecular, and chemical physics. The common manifestation of such interactions is the collective shifts of the energy levels of a many-body system. However, in a dilute thermal gas, these shifts are negligibly small compared to the Doppler broadening introduced by thermal motion, rendering their sensing challenging. Nonetheless, ultrafast nonlinear optical spectroscopy provides tools to observe subtle features of the coupling between neutral particles via measurements of the so-called multiple quantum coherence (MQC) signals.
We develop [1,2] an open quantum systems theory of MQC signals in dilute thermal gases, which accounts for the vector character of the atomic dipoles as well as for driving laser pulses of arbitrary strength, includes the far-field coupling between the dipoles, which prevails in dilute ensembles, and effectively incorporates atomic motion via a disorder average. This formalism combines earlier work of QOS on MQC [3], and on multiple scattering of light in disordered atomic samples [4].
[1] B. Ames, E. G. Carnio, V. N. Shatokhin, A. Buchleitner, New J. Phys. 23, 013024 (2022)
[2] B. Ames, A. Buchleitner, E. G. Carnio, V. N. Shatokhin, J. Chem. Phys. 155, 044306 (2021)
[3] M. Gessner, F. Schlawin, H. Häffner, S. Mukamel, A. Buchleitner, New J. Phys. 16, 092001 (2014) [4] T. Binninger, V. N. Shatokhin, A. Buchleitner, T. Wellens, Phys. Rev. A 100, 033816 (2019)
Gabriel Dufour
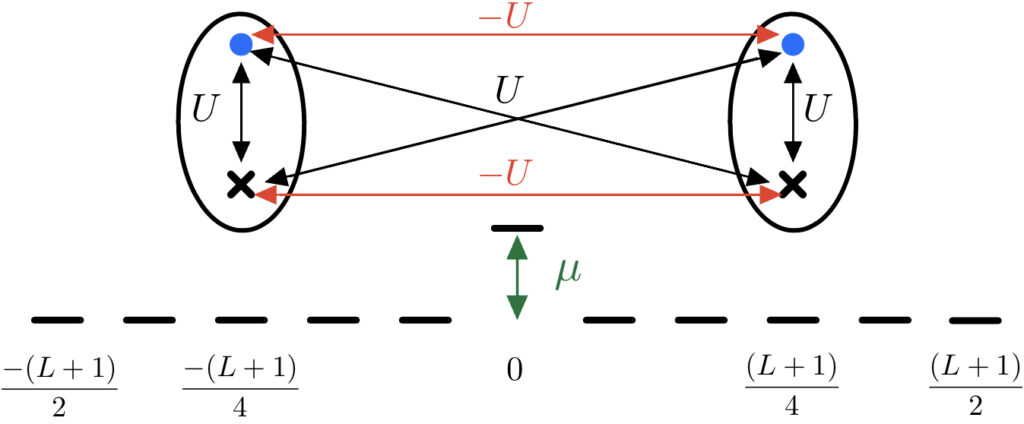
Many microscopic “particles” are actually composite objects (e.g., atoms, excitons, …). In spite of this, they typically exhibit either bosonic or fermionic behaviour. To better understand under which conditions a composite particle behaves as an elementary boson or fermion, we look at how composite particles behave in a physical scenario where the dynamics is massively affected by the quantum statistics of the particles.
For example, we consider the Hong-Ou-Mandel setup, which sees two bosons always bunch at the output of a beam splitter, whereas two fermions always leave in opposite ports, and ask what happens in the case of two composite particles each made up of two fermions.
Eric Brunner, Edoardo Carnio, Gabriel Dufour
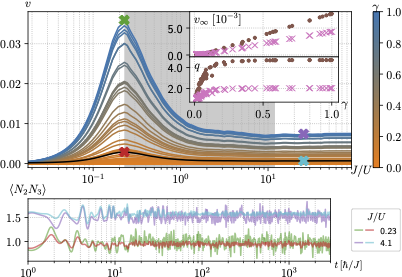
Moving away from the traditional picture of photons scattering in interferometers, we want to understand how many-particle interference manifests itself in the non-equilibrium behaviour of interacting systems, for example cold atoms in optical lattices.
Because of the interactions between the particles, such systems usually exhibit quantum chaos. The latter is typically characterised by the structure of the Hamiltonianâs spectrum and eigenstates, an approach which does not fundamentally distinguish between single and many-particle systems.
We therefore ask which signatures many-body interference leaves in the dynamics of chaotic systems, and how this is encoded in the energy spectrum and eigenstates.
Eric Brunner, Christoph Dittel, Gabriel Dufour
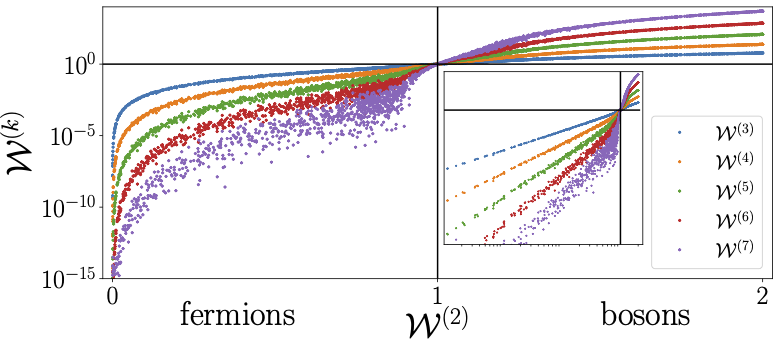
Quantum theory tells us that the universe is made out of identical particles, such that any two electrons are identical, no matter whether they live on Earth or on Alpha Centauri. In theory, such identical particles are described via completely symmetric or antisymmetric many-body wavefunctions, in which case the particles are called bosons or fermions, respectively.
Suppose now that you are given a set of identical particles which possess some internal degrees of freedom, e.g. spin or polarization. If you prepare them in the very same internal state, such that no measurement protocol can tell them apart, the particles are truly indistinguishable. This has some profound consequences for the dynamical evolution of the particles (see the research topic “Many-particle interference”).
A relevant question is how to certify the indistinguishability of a set of identical particles. If its constituents interact with an environmentthey might become – at least partially – distinguishable. We study the manifestation of partial distinguishability in the spectral and dynamical properties of interacting many-particle systems, and the implications thereof for many-particle entanglement, many-particle quantum chaos, and many-particle decoherence theory.
Andreas Woitzik

Didactics is the science of learning and teaching. In our research group, we are concerned with how we can best communicate and teach central findings from our research. We are particularly interested in how we can didactically reduce fundamental concepts from quantum mechanics and quantum optics, such as superposition or entanglement, in such a way that they can be used in school and outreach settings. Thereby we want to create connectable knowledge for later university education avoiding possible misconceptions. We examine the popular science literature for common misconceptions and are simultaneously developing teaching materials for high schools and giving training for teachers. Another research topic is the use of web applets for flexible use in the classroom and in general science communication. We have created such a web applet about a game on superposition: https://www.quantumpennyflip.com/?lang=en
